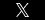A heterogeneity index and what it can tell about distributions of law firms retained, minority staff, software usage and more

A general formula for calculating heterogeneity in a group is 1-Σi2 where i is the proportion of members in the ith category. What does that mean in English? Let’s apply it to law firms retained by a department.

Let’s say a law department retained a group of 100 law firms in 2010 and for this calculation placed each firm in one of five size categories according to its number of lawyers. A category might be law firms of 1-5 lawyers, 6-15 lawyers, 16-30 lawyers, 31-99, and 100+ lawyers. It would be easy to calculate the percentage of all the 100 firms in each category. If the department retained 6 percent of its firms that were in the smallest, first category, the formula would include 6 percent squared (.0036). The next smallest category of firms (6-15 lawyers) might have, say, 7 percent so the sum would include .07 squared (.0049). You keep adding the squared percentage for each category until done, which is the meaning of the Greek letter sigma (Σ), and then subtract the total of all those category-percentages squared from 1.

If all the rest of the firms used by this department were in the fifth, largest category of firm size, there would be 87 percent in that category. Squared, 87 percent equals .7568 so the sum for each of the three categories is .765 and the difference between that sum and 1 is .235.

The higher the score on this index the more the diversity of size of law firm; the lower the score the more the firms are alike, homogeneous. To illustrate, if the fourth category had 40 percent of the firms (31-99 lawyers) and the fifth had 47 percent, the index rises substantially to .602. The law department’s retention pattern showed much more variability.

The same index could show a law department’s degree of minority lawyers by category. Or it could show the percentages of users of various software programs. The formula depicts the distribution of fees paid to law firms during a year or lawyers by office. This method to quantify the allocation of anything has much power for analytically included legal departments.