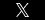More ought to be said on Bayesian statistics (See my post of Jan. 20, 2006, with its brief comment.). The breakthrough of Reverend Thomas Bayes (1702-1761), there is now even an International Society for Bayesian Analysis (ISBA).
Bayes first expressed the probability of any event – given that a related event has occurred – as a function of the probabilities of the two events independently and the probability of both events together. Bayes’ theorem can be understood in relation to the probability of being sick, given several pieces of data: a positive test result, p(sΙ+), the probability of receiving a positive test result given that one is sick, p(+׀s), the general probability of being sick, p(s), and the general probability of getting a positive result, p(+). According to Scientific Am., April 2007 at 108, Bayes’ theorem in this situation is p(sΙ+) = p(+׀s) X p(s)/ p(+). Got it?
Two examples of Bayesian calculations for law departments may help. If a law department knows that the probability of its company being sued for employment discrimination five times in any quarter is 40 percent, it knows what is referred to as a prior probability. If two discrimination cases are filed in the first month of a quarter than, Bayesian statistics allows the law department to calculate the posterior probability and its associated odds.
If a law department knows the probability of any individual lawsuit exceeding $100,000 in fees in a year, it can project how many cases of that size it is likely to face given some number of cases at the beginning of the year. If 2 percent of cases exceed that amount, and the department forecasts 40 cases in 2008, the probability is that one of the cases will exceed the mark.
 Law Department Management Blog
Law Department Management Blog