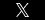Logarithms refer to exponents, the little superscript numbers that show that the base number is multiplied by itself the exponent times. Remember? 33 = 27. Logarithms are powers of 10, as as log3 is 103 = 1000. Logarithms are useful when you chart numbers that increase from tiny to very small relative to each other (See my post of .
For example, if a law department were to create a scatter gram of amounts paid to vendors during the year, the axis would contain invoices from $1 to $1 million (See my post of June 6, 2006 that explains that kind of chart.). Against that extremely wide scale (log 1 to log 6 plus), many of the smaller invoices would be barely visible, all clumped together. However, if the law department represents the amounts of bills as base-10 logarithms, the range can be readily handled.
If the second axis of the scatter gram also uses a scale of base-10 logarithms, such as to show the number of lawyers in the firms paid the invoices, the law department has felled a mighty tree, a log-log scale. Relatively straight trend lines on log scales indicate smooth increases (See my post of Aug. 9, 2006 on the Richter scale – a logarithmic scale where each additional unit is 10 times more powerful than the preceding unit – of law department cost-saving techniques.).
 Law Department Management Blog
Law Department Management Blog