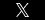In mathematics and logic, a set is a collection of items. RFPs [r], for example, are a member of the set of outside counsel management methods [M], so we could write in set notation r ∈ M. Dotted line reporting [d], another management idea, is not a member of the set of outside counsel management methods, so we would write d ∉ M.
If we think about competitive bids [c] and RFPs, they share attributes, so we can write r ∩ c to describe the overlap of those two ideas. If a selection process uses both RFPs and competitive bids, then the union of the two ideas appears as r ∪ c. Venn diagrams depict such intersections and combinations (See my post of Jan. 3, 2007: Venn diagrams; and March 9, 2007: book on history of Venn diagrams.).
Another notation describes sets as being the collection of elements with a specific property. For example, all the management initiatives that require a capital expenditure (i) would be written as set C where C = {i: i requires a capital expense} and the colon is read as “such that.” These notational grammars from set theory let us describe and think about concepts tersely and rigorously.
 Law Department Management Blog
Law Department Management Blog